第三章 数据类型和数据表示

　　这一章主要讲述计算机中所采用的数据类型，它们主要有两类：一类是基本数据类型，包括位、串、整数、实数、字符和布尔量等；另一类是结构数据类型，包括向量、数据、字符串、堆栈、队列、记录等。因为计算机只能识别"0"和"1"这些二进制位，那么在计算机中如何在存储器中用"0"和"1"来表示上面的这些数据，就是我们要学的数据表示。这一章内容不多，比较难理解的似乎是"向量"这种数据类型。本章的内容主要应掌握浮点数的数据表示。

　　一、数据类型（识记）

　　计算机中所使用的数据一般可分为三类：第一类是用户定义的数据，这类数据通常是由程序设计语言所确定的；第二类是系统数据，它是程序在执行时由计算机系统蕴含生成的；第三类是指令，即被执行的程序可看成是数据的复合。

　　上面讲的是"数据"，那么"数据类型"是什么呢？ 它不同于数据，数据类型除了指一组值的集合外，还定义了可作用于这个集合上的操作集，比如有一组整数值的集合，连同定义在这个集合上可进行的加减乘除等算术操作，这个整数的集合就成为了整数数据类型。

　　从系统结构的观点来看，数据类型可分为基本数据、结构数据、访问指针和抽象数据等类型。我们这里讲的主要是基本数据和结构数据。

　　1、基本数据类型（识记）

　　一般包括二进制位及其位串、整数及自然数、实数（浮点数）、字符和布尔数等。

　　2、结构数据类型（识记）

　　结构数据类型是一组由相互有关的数据元素复合而成的数据类型，这些数据元素可以是基本数据类型中的元素，也可以是结构数据类型本身中的元素。也就是说这些数据是有结构的，包括向量和数组、字符串、堆栈、队列、记录等，结构数据类型中的元素不一定都具有相同类型。

　　这里提到了向量，向量通常是指由标量的一组有序集合表示的量，它类似于一维数组，但又有所不同，因为标量通常只是一个整数或实数，而数组元素不一定只取实数。从计算机存储结构上来说，向量通常存储在一段连续的存储空间里。而数组元素的存储可能用链式存储方式，也就是不一定存储在连续的空间里。

　　二、数据表示

　　1、数据表示、数据类型、数据结构的关系。（领会）

　　上面我们学了数据类型，还有一个概念是数据结构，数据结构就是指上面讲结构数据类型的组织方式，它反映了结构数据类型中各种数据元素或信息单元之间的结构关系，比如树这种数据结构，里面的元素就有根和叶的层次逻辑关系。数据结构一般通过高级语言描述建立的，但是计算机硬件并不懂什么是根什么是叶，它只认0和1.这就需要我们确定如何在计算机系统中进行数据表示，让硬件能认识各种数据类型。

　　计算机系统结构中的数据表示是指可由硬件直接辨认的数据类型。这里讲到硬件直接辨认，就是说在系统中能够直接由硬件实现相应数据的运算，也就是系统结构中有相应的运算指令和运算部件来完成这项任务。那么怎么表示才能让硬件识别某种数据类型？

　　上面的数据类型和数据表示就涉及到软硬件的交界面了。数据结构所研究的是软的方面，而数据表示考虑是是硬的方面，让计算机能够识别处理，并尽量节约存储空间。

　　2、二进的定点、浮点数据表示（综合应用）

　　主要讲述是的IEEE标准的二进制浮点数表示：

　　IEEE754标准在表示浮点数时，每个浮点数均由三部分组成：符号位S，指数部分E和尾数部分M.

　　我们知道10进制数的科学计数法如A= -3.5×105

　　这里更前面有一个负号，3.5是尾数，两个有效数字，后面以10为基数的指数为5.我们可以将它表示为-3.5E5

　　同样，二进制数也可以用科学计数法规格化表示，比如5这个数，如果用二进制表示的话，整型为101，如果用科学计数法则可以表示为 1.25×24 ，这里用的是十进制，将尾数换成二进制就是1.01（就是101向前移两位小数点，和十进制完全相同），后面的指数4换成二进制则是10，那我们将其用二进制的科学计数法就可以写成1.01E10.

　　当我们依照这种计数法给一个数字确定其精度（有效位）后，就可以用一定长度的1和0的位串来表示一个实数了。

　　浮点数一般采用以下四种基本格式：

　　（1）单精度格式（32位）：除去符号位1位后，E占8位，M占23位。

　　（2）扩展单精度格式：E>=11位，M31位。

　　（3）双精度格式：（64位）；E=11位，M=52位。

　　（4）扩展双精度格式：E>=15位，M>63位。

　　我们更重要的是掌握单精度格式的表示法。在IEEE754标准中，约定小数点左边隐含有一位，通常这位数就是1，这样实际上使尾数的有效位数为24位，即尾数为1.M.指数的值在这里称为阶码，为了表示指数的正负，所以阶码部分采用移码表示，移码值为127，阶码值即从1到254变为-126至+127，在IEEE754中所有的数字位都得到了使用，明确地表示了无穷大和0，并且还引进了"非规格化数"，使得绝对值较小的数得到更准确表示。请看下表：

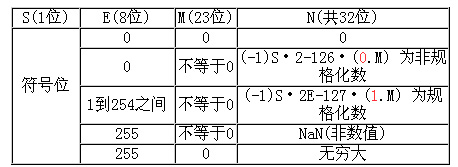
　　其中红色字0、1表示隐含位，注意当数字N为非规格化数或是0时，隐含位是0.

　　记住了上面的表格就能算出所有IEEE标准的单精度二进制浮点数了，我们重点要会计算规格化数字的双向转换，并且理解二进制浮点数表示法的思想。

　　3、向量数据表示（简单应用）

　　这里又提到向量，前面已经简单解释过向量，这里说的是向量数据表示，我们知道向量在内存中是连续存放在一段空间里的，换句话说，这些向量元素的地址是连续的。

　　在标量计算机上运行时，由于没有专门的向量数据表示，因此在计算一个向量（相当于一维数组的计算）时，每取用一个数据元素，都要用到计算该元素的地址。而在向量机中，由于有了向量数据表示，就可以把一个向量用一个位串来表示出来。向量指令就是能够用一条指令对向量的全部元素进行运算的指令。

　　比方，有两排抽屉：A和B：我们有一个任务，就是把A中每个抽屉里的东西按照顺序一一对应地搬到B的每个抽屉里。

　　用标量指令就是这样：听着，把A1抽屉里的东东给我搬到B1里去~~（等打工的搬好后……）再把A2抽屉里的东东给我搬到B2里去！（又等跑腿的搬完后……）还有，把A3抽屉……直到把全部抽屉搬好，数到了5，算是完成一项任务了，其间用了5次循环命令。

　　而用向量指令就是这么说的：听着，把A柜子从第1格抽屉起的5个抽屉的东东给搬到B柜子里去，位置是从第1格抽屉起，依次放到5个抽屉里去。这样，跑腿的就明白了，只要一句话就完成了任务。

　　向量表示就是用一个位串来表示一个向量的基址、位移量和向量长度，这样三个值就能明确表示一个向量，并能确定参加计算的元素所在的位置，因此向量表示是向量指令及向量机得以实现的基础。

　　在向量处理中，还会遇到稀疏向量（就是含有大量0元素的向量），所以为了节省空间了处理时间，采用压缩向量的表示方法。这里要注意的是有一个中间向量Z向量，它是一个位向量，每个元素不是1就是0，而压缩向量就是根据Z向量中的有1的元素对应的稀疏向量元素存储起来而得到的。这个容易理解。

　　4、自定义数据表示（领会）

　　为了减少高级语言与机器语言之间的差别，采用了自定义数据表示，就是由数据本身来表明数据类型，这样可以使每种指令的种类大为减少，称为通用化指令。自定义数据表示形式有两种，即带标志符数据表示和数据描述符表示。

　　带标志符数据表示就是对每一个数据都附加一个标志符，由这个标志符来表示这个数据的类型。这种表示法有它的优点也有它的缺点，请认真领会一下。

　　其优点是：简化指令系统；易于对编程查错；自动类型转换；简单化编译；方便程序调试。缺点是增加存储空间又使指令执行速度变慢。

　　另一种就是数据描述符表示，主要用来描述复杂和多维结构的数据类型，如向量、记录等，它于带标志符数据表示不同之处是：

　　（1）标志符要与每个数据相连，两者合存在一个存储单元中；而描述符则和数据分开存放（一个连合一个分）

　　（2）要访问数据集中的元素时，必须先访问描述符，这就至少增加一级寻址（先访描符增寻址）

　　（3）描述符可看成是程序一部分，而不是数据的一部分。标志符则可看作是数据的一部分（程序部分不是数）