自考365网给大家整理了2020年8月自考公共课《线性代数（经管类）》试题及答案解析，一起来试试吧！

说明：在本卷中，A^T表示矩阵A的转置矩阵，A*表示矩阵A的伴随矩阵，E是单位矩阵，|A|表示方阵A的行列式．r(A)表示矩阵A的秩.

扫码入群>>获取自考公共课全套试题及答案解析

2020年8月线性代数（经管类）自考试题及答案解析

一、单项选择题

1. 设α₁,α₂,β₁,β₂是3维列向量，且行列式|α₁,α₂,β₁|=m，|α₁,β_2,α₂,|=n，，则行列式|α₁,α₂,β₁＋β₂|=（　）。

2.设A为3阶矩阵，将A的第2列与第3列互换得到矩阵B，再将B的第1列的（-2) 倍加到第3列得到单位矩阵E，则A-¹=

3. 设向量组α₁,α₂,α₃线性无关，而向量组α₂,α₃,α₄线性相关，则（　）。

4.若3阶可逆矩阵A的特征值分别是1,-1, 2，则|A-¹|＝（　）。

5. 二次型f(x₁,x₂,x₃)=x₂²+2x₁x₃的规范形是（　）。

二、填空题

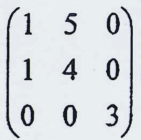
6. 已知行列式D=，其代数余子式为A_ij(i,j=1,2,3,4)，则3A₁₁+6A₁₂-7A₁₃+8A₁₄=                 .

7.行列式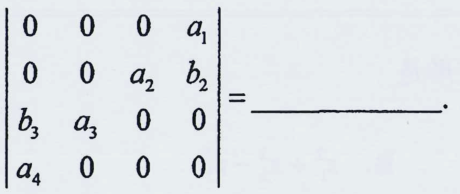

8. 设矩阵，若矩阵A满足AP₁P₂=B，则A=                 .

9. 已知矩阵A=，则A^-1=                 .

10. 设向量组α₁=(1,1,a)^T，α₂=(1,a,1)^T，α₃=(a,1,1)^T的秩为3，则数a的取值应满足                  .

11. 与向量α₁=(1,1,1)^T，α₂=(1,2,-1)^T都正交的任意非零向量α=                   .

12. 设A为3×4矩阵，r(A)=3，若η₁，η₂为非齐次线性方程组Ax = b的解且η_1≠η₂, 则其导出组Ax = 0的通解为x=                   .

13. 若线性方程组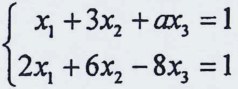无解，则数a＝                   .

14.设2阶矩阵A与B相似，若A的特征值为-3和2，则|B²|＝                   .

15.二次型f(x₁,x₂,x₃)=(5x₁²+x₂²+ax₃²+4x₁x₂－2x₁x₃－2x₂x₃正定，则数a的取值范围为                   .

三、计算题

16.设α₁,α₂,α₃为2维列向量，令A=(α₁,α₃)，B=(2α₂,3α₃)，且已知|A|=½,|B|=-2， 求行列式|A+B|的值。

17. 已知矩阵A=，求2A²+3A-4E.

18.已知矩阵A=，求A^-1.

19.求向量组α₁=(1,-1,2,1)^T， α₂=(1,0,2,2)^T，α₃=(0,2,1,1)^T， α₄=(1,0,3,1)^T，α₅=(-1,5,-1,2)^T的秩和一个极大线性无关组，并将向量组中的其余向量由该极大线性无关组线性表出.

20. 设4元非齐次线性方程组Ax = b的增广矩阵经初等行变换化为，讨论a、c为何值时方程组有无穷多解并求出其通解（要求用其一个特解和导出组的基础解系表示）.

21. 设矩阵A=，试判定A是否可对角化，并说明理由.

22.已知二次型f(x₁,x₂)=-3x₁²+4x₁x₂分别经可逆线性变换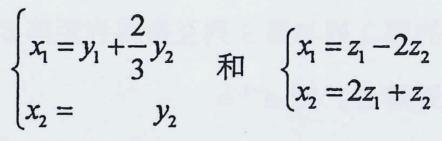化为标准形Ⅰ与Ⅱ.求

(1)标准形Ⅰ与Ⅱ； 

(2）可逆线性变换y = Cz,将标准形Ⅰ化为标准形Ⅱ.

二、简答题

23.设A为n阶矩阵，α₁,α₂分别是A的属于特征值λ₁,λ₂的特征向量，且λ_1≠λ₂. 证明当λ_1,λ₂均不为零时，向量组Aα₁,Aα₂线性无关．

2020年自学考试题库已上线，赶快刷起来>>

自考365提供从报名到毕业一站式服务！【点击咨询>> 】